
În calcul, operațiile logice sunt necesare deoarece ele pot fi folosite pentru a modela modul în care informațiile circulă prin circuite electrice, cum ar fi circuitele din interiorul unui procesor. Aceste tipuri de operațiuni se numesc operații booleene.
Elementele dintr-un circuit care se comportă în conformitate cu logica booleană se numesc porți logice.
Operații logice fundamentale
Următoarele șapte operații logice iau intrări care sunt fie true (1), fie false (0) și produc o singură valoare de ieșire care este, de asemenea, adevărată sau falsă.
Cele mai multe dintre aceste operațiuni pot necesita mai mult de două intrări, cu excepția operației NOT care are doar o singură intrare. Mai jos sunt exemple utilizând doar una sau două intrări, ceea ce se întâmplă de obicei în interiorul unui computer.
Operațiile sunt listate mai jos. Faceți clic pe un link pentru o operație pentru a afla mai multe.
- ȘI
- SAU
- NU
- NAND
- NICI
- XOR
- XNOR
Operația logică ȘI returnează adevărat numai dacă toate intrările sunt adevărate. Dacă oricare dintre intrări este falsă, ieșirea este de asemenea falsă.
În programarea pe calculator, operația AND este de obicei scrisă ca && (două ampersands).
În algebra booleană, operația AND a două intrări A și B poate fi scrisă ca AB .
Mai jos este tabelul de adevăr pentru o operație cu două intrări AND și schema de circuit a unei porți logice AND.

| ȘI | ||
|---|---|---|
A | B | AB |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
SAU
Operația logică OR returnează adevărat dacă oricare din intrările sale sunt adevărate. Dacă toate intrările sunt false, ieșirea este de asemenea falsă.
În programarea pe calculator, operația OR este de obicei scrisă ca || (două bare verticale).
În algebra booleană, valoarea OR a două intrări A și B poate fi scrisă ca A + B.
Notă: Nu confundați operația OR pentru adăugarea aritmetică, chiar dacă ambele utilizează simbolul " + ". Sunt operațiuni distincte.
Mai jos este tabelul de adevăr pentru o operație OR cu două intrări și schema de circuit a unei porți logice OR.

| SAU | ||
|---|---|---|
A | B | A + B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
NU
Operația NOT logică revine adevărată dacă intrarea ei este falsă și false dacă intrarea sa este adevărată.
În programele de calculator, operația NOT este de obicei scrisă ca ! (un semn de exclamare).
În algebra booleană, valoarea NOT a unei intrări A poate fi scrisă ca A ^ (A cu o suprascore).
Mai jos este tabelul de adevăr pentru o operație NOT și schema de circuit a unei porți logice NOT.

NAND
Operația logică NAND (care reprezintă "NOT AND") returnează adevărat dacă oricare dintre intrările sale sunt false și false dacă toate intrările sunt adevărate.
În algebra booleană, valoarea NAND a două intrări A și B poate fi scrisă ca

NAND are distincția de a fi una dintre cele două porți logice "universale", deoarece orice altă operație logică poate fi creată utilizând doar porți NAND. (Cealaltă poartă logică universală este NOR.)
Mai jos este masa de adevăr pentru o operație NAND cu două intrări și schema de circuit a unei porți logice NAND.

| NAND | ||
|---|---|---|
A | B | ___ AB |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
NICI
Operația logică NOR (care reprezintă "NOT OR") este adevărată dacă toate intrările sale sunt false și false dacă oricare din intrările sale sunt adevărate.
În algebra booleană, valoarea NOR a două intrări A și B poate fi scrisă ca
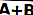
NOR are distincția de a fi una dintre cele două porți logice "universale", deoarece orice altă operație logică poate fi creată numai cu porți NOR. (Cealaltă poartă logică universală este NAND.)
Mai jos este masa de adevăr pentru o operație NOR cu două intrări și schema de circuit a unei porți logice NOR.

| NICI | ||
|---|---|---|
A | B | _____ A + B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOR
Operația logică XOR (care reprezintă "Exclusive OR", returnează adevărat dacă oricare dintre intrările ei diferă și false dacă sunt toate aceleași. Cu alte cuvinte, dacă intrările sale sunt o combinație de true și false, ieșirea XOR este adevărat.Dacă intrările sale sunt toate adevărate sau toate false, ieșirea de XOR este falsă.
În algebra booleană, valoarea XOR a două intrări A și B poate fi scrisă ca A⊕ B. (Simbolul XOR, ⊕, seamănă cu un semn plus într-un cerc.)
Mai jos este tabelul de adevăr pentru o operație XOR cu două intrări și schema de circuit:

| XOR | ||
|---|---|---|
A | B | A⊕B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XNOR
Operația logică XNOR (care înseamnă "Exclusive NOT OR" se întoarce dacă toate intrările sunt aceleași și false dacă diferă oricare dintre ele. Cu alte cuvinte, dacă intrările sale sunt o combinație între true și false, ieșirea din XNOR este falsă. Dacă intrările sale sunt toate adevărate sau toate false, ieșirea din XNOR este adevărată.
În algebra booleană, valoarea XNOR a două intrări A și B poate fi scrisă ca

Mai jos este tabelul de adevăr pentru o operație XNOR cu două intrări și schema de circuit:

| XNOR | ||
|---|---|---|
A | B | _____ A⊕B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
- Cum creez un program de calculator?
Acumulator, Boolean, Idempotence, Operator, Termeni de programare
